The Parallel System

Each benchmark from the Parallel LTL track is based on a parallel system of (rooted) Labeled Transition Systems (LTSs) that communicate via synchronized transitions. A labeled transition system consists of a set of states, a start state, an alphabet of transition labels, and a transition relation that connects states via labeled transitions. It can be perceived as an automaton with actions written onto its transitions. Within the Parallel LTL track of RERS, the alphabet of an LTS always equals the union of all transition labels that occur in it. The following image shows a parallel system of three LTSs.

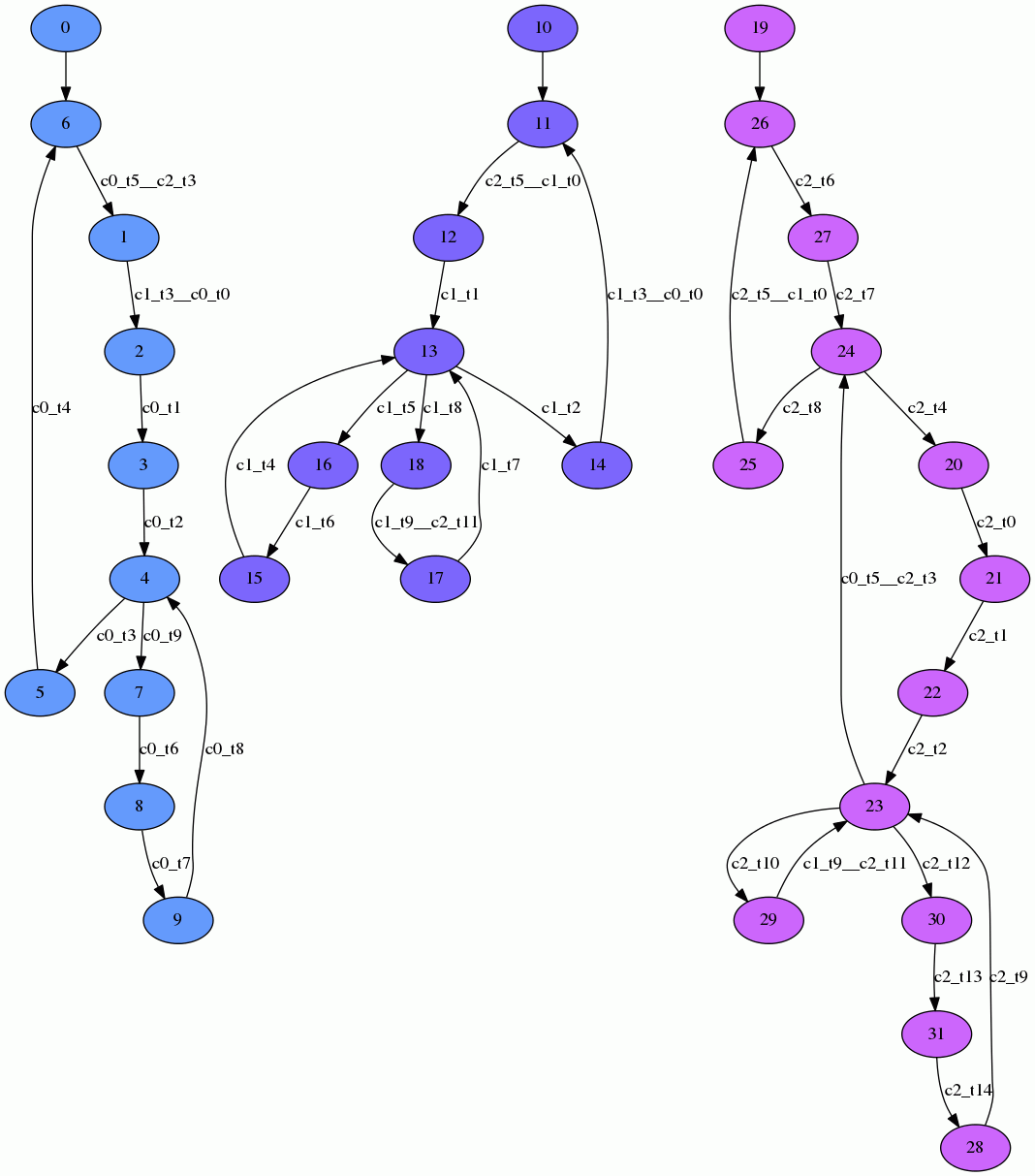
The semantics of a parallel system of LTSs is formally defined as follows:

Intuitively speaking, a transition with label l is feasible in the parallel composition if and only if all LTSs that contain label l feature an outgoing transition labeled l from their current state. Given a benchmark from the challenge, the associated LTL properties have to be checked on the parallel composition of all LTSs in that benchmark system, more precisely on all infinite traces of this parallel composition.

For RERS 2017, up to two parallel LTSs share a common alphabet, meaning that all existing communication is pair-wise and unbuffered synchronous (rendezvous) communication. The sole exeption are transitions with an empty label that occur once in every LTS. They encode the start state of each LTS which is defined as the target of the single transition with an empty label. Whether or not empty labels are considered as part of a trace is irrelevant to the analysis of the provided LTL properties. No two transitions with different labels can ever be triggered at the exact same time, however multiple interleavings might be possible.

---

Provided Files

Each benchmark problem is available in three different formats:

1. Process graphs (.dot file) that directly represent the system of parallel LTSs described above. Such a file can therefore be used to check the LTL properties and to visualize the parallel system (for example using the tool Graphviz, command line: "dot -Tpdf problemX.dot -o problemX.pdf")
2. An implementation of the parallel system in Promela. This version already includes the list of LTL properties and can therefore be used to check the validity of these properties, for example when provided as input to the verification tool SPIN. For simplicity, both the automaton-internal transitions and the communication with the environment are triggered by an "Environment" process that sends messages non-deterministically. The automaton-internal transitions labeled with an empty string in the LTS specification are relabeled to "nop", indicating that no action occurred. A "Listener" process is notified about every occurring communication and always sets the global variable "lastAction" to the label of the most recently triggered transition(s).
3. A formal definition of the system as a Petri net. The syntax used is the Petri Net Markup Language (PNML) that was already used in other verification challenges. Please note that the transition names in a PNML file represent the labels of LTL traces, not the transition IDs.

The LTL properties are already included within the Promela files and also provided in a separate .txt file.

---

LTL Properties

The LTL properties that participants have to analyze constrain the behavior of the given parallel system based on its feasible infinite action traces. Whenever a transition is triggered, the corresponding label represents the current action. Because only infinite traces are considered, no finite trace can ever violate an analyzed LTL property. Detailed information regarding the used LTL syntax and its semantics can be found at the SPOT library website.

A trace of a parallel system is defined as the sequence of actions (labels from triggered transitions): The first transition that occurred is true at the first state in the trace, the second triggered transition at the second state in the trace, and so on. Whether or not transitions with an empty label are included in this trace (and whether or not they are perceived as synchronized transitions) is irrelevant for this challenge.

Because only one transition can be triggered at a given time step, transition labels other than the one from the triggered transition do not hold at that state in the trace. For example, consider a parallel system with the global alphabet of transition labels {"a","b","c"}. Let us assume the following action sequence (transition label trace):

 "a" -> "b" -> "a" -> "c" ...

The trace of states that the LTL property has to be evaluated on would then start as follows ('!' representing negation):

 ("a" & !"b" & !"c") -> (!"a" & "b" & !"c") -> ("a" & !"b" & !"c") -> 
(!"a" & !"b" & "c") ...

A parallel system satisfies a given LTL property if and only if all of its feasible infinite action traces satisfy that property.