Parallel Problem Description
The Parallel System
Each benchmark from the Parallel LTL track is based on a parallel system of (rooted) Labeled Transition Systems (LTSs) that communicate via synchronized transitions. A labeled transition system consists of a set of states, a start state, an alphabet of transition labels, and a transition relation that connects states via labeled transitions. It can be perceived as an automaton with actions written onto its transitions. Within the Parallel LTL and Parallel CTL tracks of RERS, the alphabet of an LTS always equals the union of all transition labels that occur in it. Note that in contrast to the problems from the Sequential LTL and Sequential Reachability tracks, the alphabet of our parallel systems is not split into input and output symbols. The following image shows a parallel system of three LTSs.
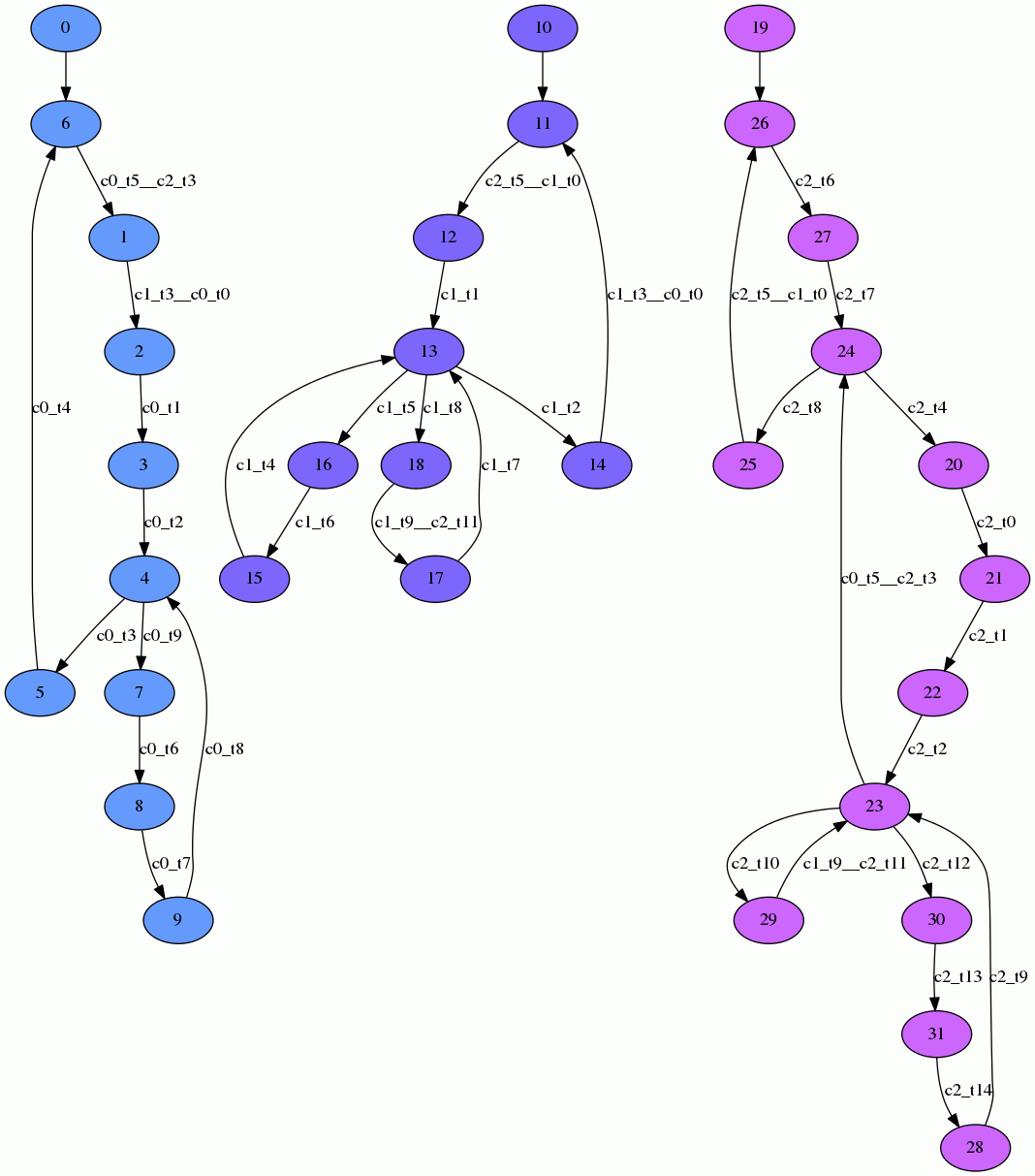
The semantics of a parallel system of LTSs is formally defined as follows:

Intuitively speaking, a transition with label l is feasible in the parallel composition if and only if all LTSs that contain label l feature an outgoing transition labeled l from their current state. Given a benchmark from the challenge, the associated LTL properties have to be checked on the parallel composition of all LTSs in that benchmark system (details can be found below).
The target of a transition with an empty label is the start state of the respective LTS. Whether or not empty labels are considered as part of a trace is irrelevant to the analysis of the provided LTL properties. No two transitions with different labels can ever be triggered at the exact same time, however multiple interleavings might be possible.
Provided Files
Each benchmark problem is available in three different formats:
- Process graphs (.dot file) that directly represent the system of parallel LTSs described above. Such a file can therefore be used to check the LTL properties and to visualize the parallel system (for example using the tool Graphviz, command line: "dot -Tpdf problemX.dot -o problemX.pdf")
- An implementation of the parallel system in Promela. This version already includes the list of LTL properties and can therefore be used to check the validity of these properties, for example when provided as input to the verification tool SPIN. For simplicity, both the automaton-internal transitions and the communication with the environment are triggered by an "Environment" process that sends messages non-deterministically. The automaton-internal transitions labeled with an empty string in the LTS specification are relabeled to "nop", indicating that no action occurred. A "Listener" process is notified about every occurring communication and always sets the global variable "lastAction" to the label of the most recently triggered transition(s).
- A formal definition of the system as a Petri net. The syntax used is the Petri Net Markup Language (PNML) that was already used in other verification challenges. Please note that the transition names in a PNML file represent the labels of LTL traces, not the transition IDs.
The LTL properties are already included within the Promela files and also provided in a separate .txt file.
LTL Properties
The Parallel LTL track of RERS 2019 features two different semantics regarding its LTL properties. This decision is based on the available Promela version which traditionally coincides with a different interpretation of finite traces.Petri net (.pnml) and Parallel LTSs (.dot):
The LTL properties that participants have to analyze constrain the behavior of the given parallel system based on its feasible infinite action traces. Whenever a transition is triggered, the corresponding label represents the current action. Because only infinite traces are considered, no finite trace can ever violate an analyzed LTL property. Detailed information regarding the used LTL syntax and its semantics can be found at the SPOT library website.
A trace of a parallel system is defined as the sequence of actions (labels from triggered transitions): The first transition that occurred is true at the first state in the trace, the second triggered transition at the second state in the trace, and so on. Whether or not transitions with an empty label are included in this trace (and whether or not they are perceived as synchronized transitions) is irrelevant for this challenge.
Because only one transition can be triggered at a given time step, transition labels other than the one from the triggered transition do not hold at that state in the trace. For example, consider a parallel system with the global alphabet of transition labels {"a","b","c"}. Let us assume the following action sequence (transition label trace):
"a" -> "b" -> "a" -> "c" ...The trace of states that the LTL property has to be evaluated on would then start as follows ('!' representing negation):
("a" & !"b" & !"c") -> (!"a" & "b" & !"c") -> ("a" & !"b" & !"c") ->
(!"a" & !"b" & "c") ...
A parallel system satisfies a given LTL property if and only if all of its
feasible infinite action traces satisfy that property.
Promela (.pml):
If you indicate that you have analyzed the Promela version of the parallel benchmarks in your submission email, then we expect that you have checked the given LTL properties according to the semantics of the tool SPIN. The LTL properties are included in the respective .pml file. Note that the LTL semantics of SPIN differ from our usual definition where only infinite paths are considered. In case that you analyze the Promela version of the benchmarks, however nonetheless apply our usual LTL semantics where only infinite paths are considered, please explicitly state this in your submission email.
CTL Properties
The properties from the Parallel CTL track are explained in the following. In contrast to the Parallel LTL track, CTL properties have to be checked on all branches of the expanded parallel composition, including those that end eventually. Whereas the LTL properties of RERS only constrain infinite traces, branches that lead to finite paths have to be considered for CTL properties. This includes those that lead into a deadlock.Syntax
The syntax of CTL properties used within the RERS Challenge 2019 is defined by the following Backus-Naur form:
f::= 'true' | 'false' | f '&' f | f '|' f | f '=>' f | f '<=>' f
| '[]' f | '<>' f | '['a']' f | '<'a'>' f
| 'A(' f 'U' f ')' | 'E(' f 'U' f ')'
| 'A(' f 'W' f ')' | 'E(' f 'W' f ')'
| 'AG' f | 'EG' f | 'AF' f | 'EF' f
where each occurrence of a represent any transition label.
Semantics
The corresponding semantics adhere to usual definitions and can mostly be found in textbooks or papers such as this one. The formula "[] f" replaces "AX f" and "<> f" replaces "EX f". U stands for "strong until" whereas W stands for "weak until".
Note that the above syntax does not include individual atomic propositions: State predicates cannot be expressed using this definition. This matches the fact that we constrain the behavior of transition systems instead of Kripke structures.
Instead, it is possible to express that a formula f has to hold on certain successor states: The formula "[a] f" is true in state s if all outgoing transitions of s labeled with a lead to states that satisfy the formula f. Similarly, the formula "<a> f" holds in state s if there exists an outgoing transition of s labeled with a whose target state satisfies formula f.
Model Checking
A parallel system of (rooted) LTSs satisfies a CTL formula f if and only if the start state of the corresponding expanded parallel composition satisfies f (see above).