Parallel Problem Description
The RERS Challenge 2016 provides a wealth of parallel benchmark problems of increasing complexity, for which the overall complexity for state-of-the-art tools is unknown. The benchmarks are synthesized to exhibit chosen properties, but were not modified like their sequential counterparts.
The benchmark difficulty in this track increases according to the number of parallel components in each system. This number is identical to the last two digits of the problem's number. The first five benchmarks contain 1 through 5 parallel transition systems respectively and can be analyzed completely using existing tools such as SPIN. These problems still count towards the participant's score. Results of such existing tools can be submitted and used as a reference for participants' own verification tools. The code language is Promela.
The Parallel System
Each automaton in a parallel system is formalized as a labeled transition system. The automata interact with each other and with the environment outside of the parallel system via pair-wise and unbuffered synchronous (rendezvous) communication. This type of communication is encoded in the labeling of the automata's transitions: If the label of a transition exists twice in the parallel system, then these transitions can only be triggered simultaneously. The only exception to this rule are transitions that are labeled with an empty string, they imply an automaton-internal transition that can be triggered from its source state at anytime. No two transitions can ever be triggered at the exact same time, however multiple interleavings might be possible.
The automata represent the complete communication skeleton of the parallel system, actual parallel computation could occur whenever a state of an automaton is reached. This truly parallel computation does not affect the possible communication patterns and is therefore not modeled within the benchmarks.
All labels that are unique in a parallel system are understood as a response to input from the environment. The environment is known to always eventually provide the parallel system with input that triggers a transition in the system, unless the entire parallel system encountered a deadlock. The following image shows a parallel system with 3 synchronized automata.
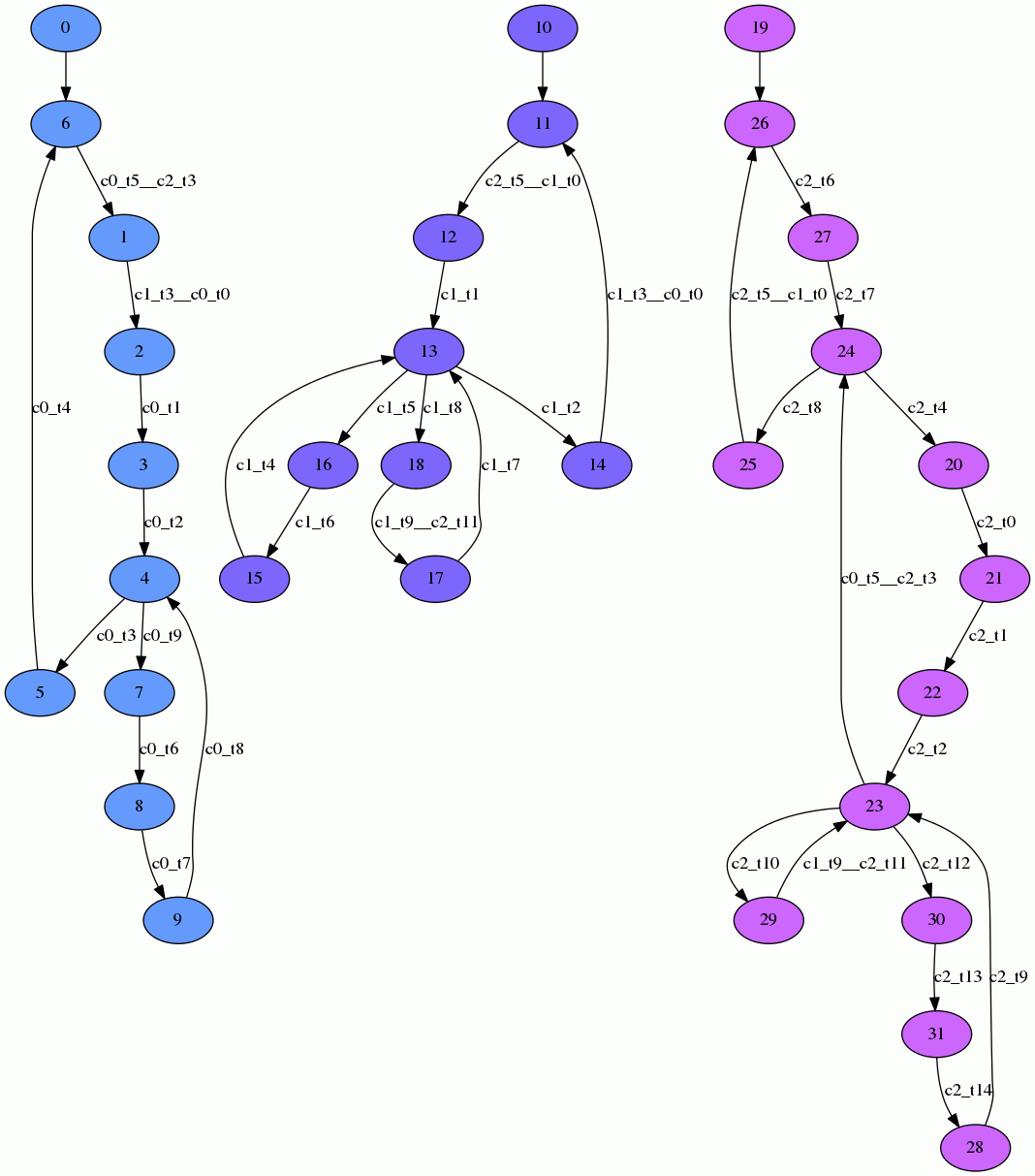
LTL Properties
The LTL properties that participants have to analyze constrain the behavior of the given parallel system based on its feasible communication traces. This is a comprised description of the semantics and syntax, detailed information can be found at the SPOT library website.
A trace of a parallel system is defined as the sequence of labels from triggered transitions: The first transition that occurred is true at the first state in the trace, the second triggered transition at the second state in the trace, and so on. Automaton-internal transitions with an empty label are included in this trace.
Because only one transition can be triggered at a given time step, transition labels other than the one from the triggered transition do not hold at that state in the trace. For example, consider a parallel system with the global set of transition labels {"","a","b"}. Let us assume the following transition label sequence (communication trace):
"" -> "b" -> "" -> "a" ...The trace of states that the LTL property has to be evaluated on would then start as follows ('!' representing negation):
("" & !"a" & !"b") -> (!"" & !"a" & "b") -> ("" & !"a" & !"b") ->
(!"" & "a" & !"b") ...
A parallel system satisfies a given property if and only if all of its
feasible traces satisfy that property.